Topological inference for subdivision schemes

Introduction

In this post, we explain how to retrieve the topological part of a subdivision scheme as a graph transformation rule.

We represent objects with generalized maps (or G-map), a formalization of edge-based models for non-oriented quasi-manifolds. A G-map consists of a collection of topological cells (vertices, edges, faces, volumes, etc.) and the incidence and adjacency relation between these cells.

We design modeling operations as rules from the theory of graph rewriting. Therefore, an operation consists of a left-hand side (LHS) and a right-hand side (RHS). The LHS describes the part of the object that should be found in the object to apply the operation. The RHS depicts the result of the operation, i.e., elements present in the object after the application of the operation.

The cells are encoded via orbits, i.e., subgraphs induced by a subset of dimensions. These cells play two key roles:

• They allow the generalization of graph transformation rules to define modeling operations up to some topological redundancies.
• They support the definition of embeddings, i.e., the geometric information.

Inferring a subdivision scheme

A subdivision scheme consists of a topological refinement and a geometric smoothing. The topological folding algorithm [1] offers a solution to retrieve the topological part of the operation. We now provide a tool and some guidelines to realize the inference of the topological part of some subdivision schemes. The geometric computations are given below.

Some more information may be found here, where we explain how to infer the topological part of geometric modeling operations for an application in geology.

Executable

Here is an executable that you can use to infer operations (compiled on 01/01/2022).

Installation and Usage

Extract the zipped folder and run the jar.

Java conflicts

JerboaStudio’s viewer runs with JOGL, which is no longer supported on macOS. JOGL also seems to conflict with OpenJDK on Linux distributions and Java versions over Java 11 but runs smoothly with the JDK 11 from Oracle.

Source code

JerboaStudio’s source code is available via GitLab, with instructions to build and run the compiled executable.

Demo

Quad subdivision

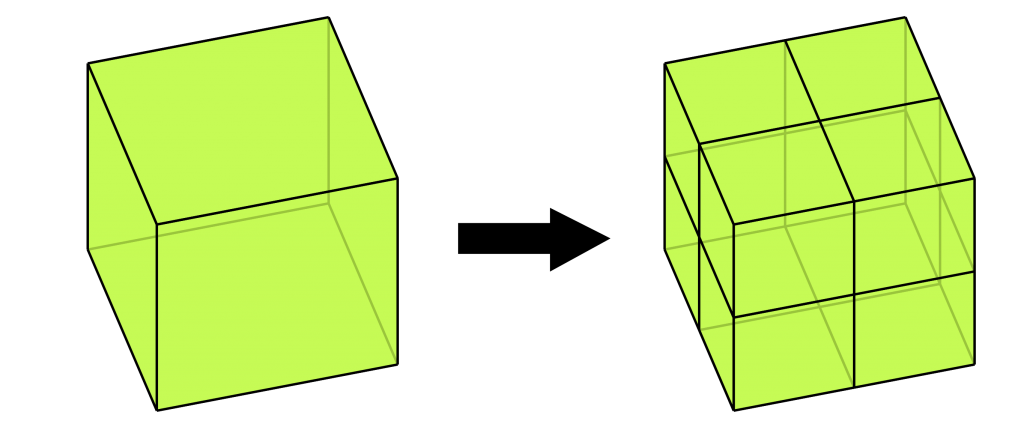
Embedding expressions:

• Node for edge points:

return Point3::middle(<0>_position(n0));

• Node for face points:

return Point3::middle(<0,1>_position(n0));

Catmull-Clark

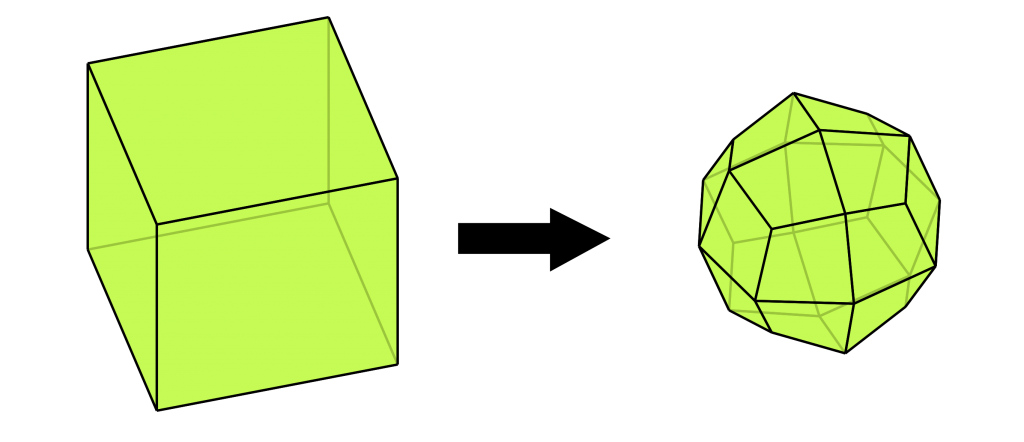
Embedding expressions:

• Node for vertex points:

JerboaList <@ebd<position>> new_face_points;
for(JerboaDart d : <1,2,3>_<0,1,3>(n0)) {
    new_face_points.add(Point3::middle(<0,1>_position(d)));
}
Point3 avg_face_points = Point3::middle(new_face_points);

int n = 0;
JerboaList <@ebd<position>> old_edge_midpoints;
for(JerboaDart d : <1,2,3>_<0,2,3>(n0)) {
    old_edge_midpoints.add(Point3::middle(<0>_position(d)));
    n = n+1;
}
Point3 avg_edge_points = Point3::middle(old_edge_midpoints);

Point3 old_coord = new Point3(n0.position);

double scalingQ = 1.0 / n;
avg_face_points.scale(scalingQ);

double scalingR = 2.0 / n;
avg_edge_points.scale(scalingR);

double scalingS = (n - 3.0) / n;
old_coord.scale(scalingS);

old_coord.add(avg_face_points);
old_coord.add(avg_edge_points);
return old_coord;

• Node for edge points:

Point3 face1Mid = Point3::middle(<0,1>_position(n0));
Point3 face2Mid = Point3::middle(<0,1>_position(n0@2));
Point3 faceMid = Point3::middle(face1Mid, face2Mid);
Point3 edgeMid = Point3::middle(<0>_position(n0));
return Point3::middle(faceMid, edgeMid);

• Node for face points:

return Point3::middle(<0,1>_position(n0));

Loop

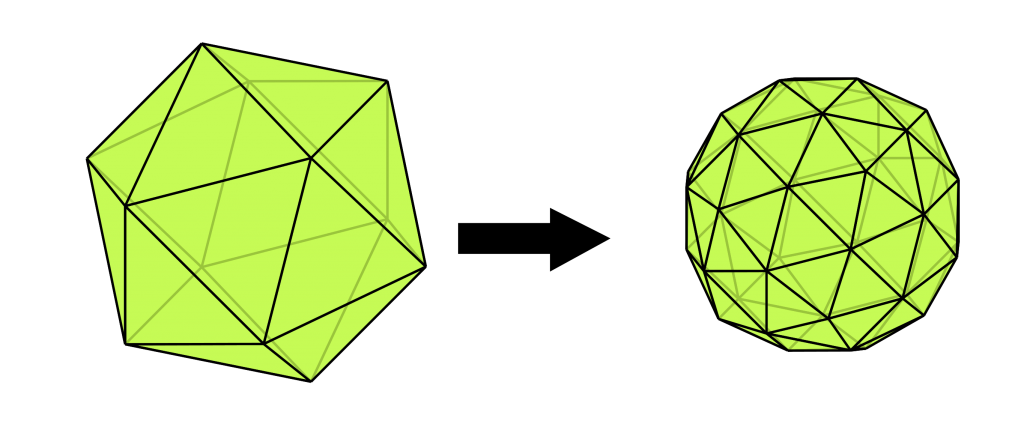
• Node for vertex points:

int n = 0;
JerboaList <@ebd<position>> sommetsAdjacents ;
for (JerboaDart d : <1,2>_<2>(n0)) {
    sommetsAdjacents.add(d@0.position);
    n = n+1;
}
Point3 bary = Point3::middle(sommetsAdjacents);

if (n==2){
    return Point3::barycenter(n0.position, 3.0/4.0, bary, 1.0/4.0);
}
else if (n==3){
    return Point3::barycenter(n0.position, 7.0/16.0, bary, 9.0/16.0);
}
else {
    return Point3::barycenter(n0.position, 5.0/8.0, bary, 3.0/8.0);
}

• Node for edge points:

return Point3::barycenter(n0.position, 3.0/8.0, n0@0.position, 3.0/8.0, n0@1@0.position, 1.0/8.0, n0@2@1@0.position, 1.0/8.0);

Butterfly

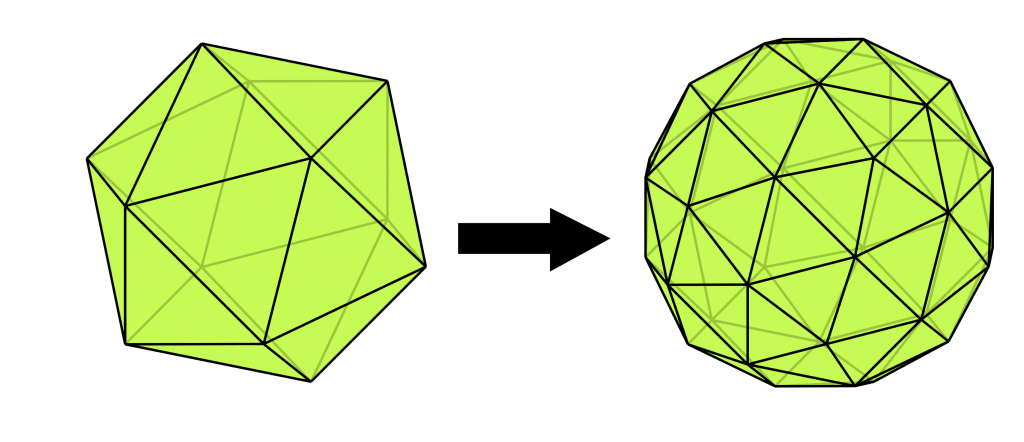
• Node for edge points:

// Param
double w = 1.0/16.0;

// Edge points
Point3 correctedMiddle = Point3::middle(n0.position, n0@0.position);

// Adajacent points in the faces
Point3 facePoint = new Point3();
for (JerboaDart d : <0,2>(n0)) {
    facePoint.add(d@1@0.position);
}
// facePoint.scale(2);
// No need to scale since we consider the four darts of the edge

// Opposite points in adjacent faces
Point3 oppPoint = new Point3();
for (JerboaDart d : <0,2>(n0)) {
    oppPoint.add(d@1@2@1@0.position);
}
oppPoint.scale(-1);

// s point
Point3 s = new Point3();
s.add(facePoint);
s.add(oppPoint);
s.scale(w);

// edge + ws
correctedMiddle.add(s);
return correctedMiddle;

Doo-Sabin

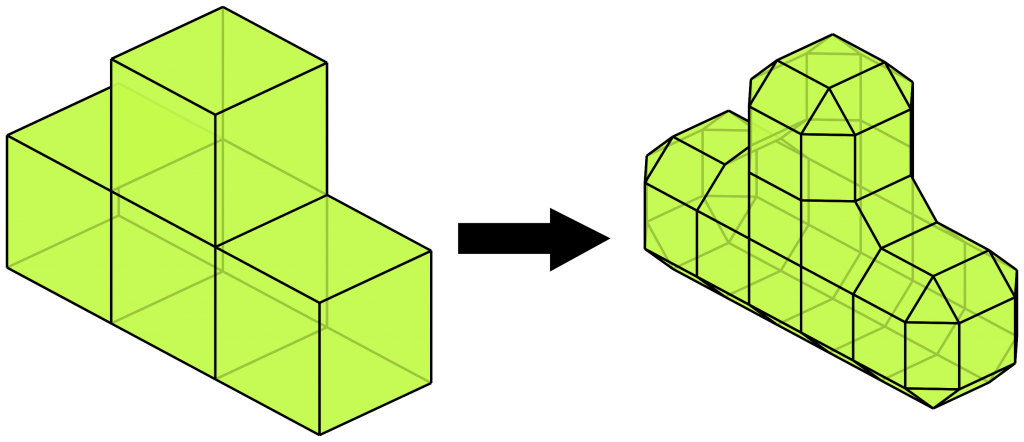
• Node for vertex points:

Point3 centerFace = Point3::middle(<0,1>_position(n0));
Point3 midEdge1 = Point3::middle(<0>_position(n0));
Point3 midEdge2 = Point3::middle(<0>_position(n0@1));
return Point3::middle(centerFace, midEdge1, midEdge2, n0.position);