Lesson 2: Discover embeddings and orbits

Pages

In this lesson you will discover embeddings and orbits which are integral to properly using G-maps and the Jerboa modeler editor. You will use the same modeler as you did for the first lesson and the specific operations can be found in the « Lesson2 » folder.

UNDERSTANDING EMBEDDINGS

Objects are defined by their topological structure (see lesson 1) and different geometric, physical or applicative characteristics called embeddings. In this example modeler there are two types of embedding:

geometric: 3D points associated with vertices
physical: color defined by RGB values and associated to face sides

The embeddings of the topological structure associate characteristics. In this example modeler each dart has two embeddings:

a geometric point: instance of the « Points » java class
a color: instance of the « Color » java class

delete the previous models by opening file and clicking on new in file
execute “c-IcositeHexagon”, you should see the Screen 2.1

You can select a dart and then observe all of it’s details in the window to the right of the screen. One of those details is the list of embeddings.

Color is a property of a face side so it is embedded in the volume face, this means that every dart which belongs to a given volume and face contains the information of its color.

Geometric points are a property of vertices so they are embedded in the vertex, which means that every dart of a vertex contains the geometric point of that vertex.

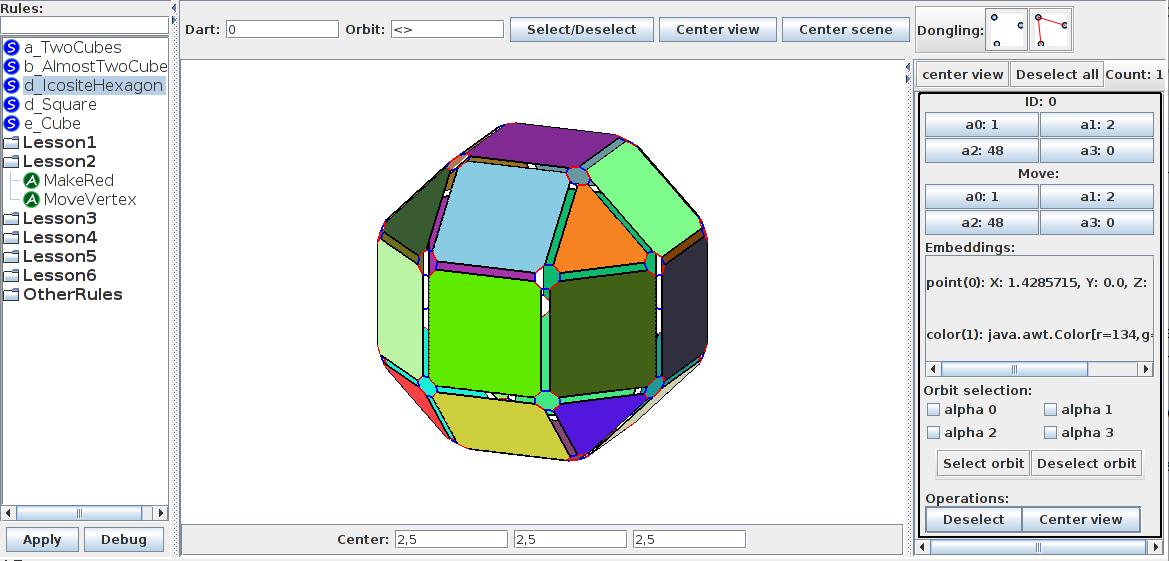
compare embeddings
- select the “0” dart and look at the value of the point embedding
- select the “20” dart and compare the point embedding to that of the “0” dart

UNDERSTANDING ORBITS

Certain parts of an object have different values of each embedding (each vertex of an object has a different position, each face can have a different color) which are associated with every dart which belongs to that particular part of the object. The part of the object is a topological cell or more generally an orbit. For example a point is associated with a vertex cell and a color is associated with a volume face (not with the whole face cell, this means that face can have a color on each side).

An orbit can be obtained by selecting a dart and a set of link’s numbers. The obtained orbit is a sub-graph of the object’s topological structure (which is a graph), containing the selected dart itself, all the darts which are connected to it by a particular path of links with the given numbers and those links themselves.

You can select a sub-graph thanks to it’s orbit using the dart selection tool at the top of the screen by entering an orbit as well as a dart.

in the dart selection tool enter 15 in the « Dart » text field and <0,1> in the « Orbit » text field
observe the selected darts, you should have selected a volume face containing dart 15
deselect these darts and select the darts from dart 15 with the orbit <α0,α2,α3>, you should have selected the edge containing dart 15

EMBEDDINGS AND THEIR ORBITS

figure out which orbit contains the color embedding
- select dart “0“
- execute the “MakeRed” operation
- select the red volume face using the correct dart and orbit (<α0,α1>)

figure out which orbit contains the point embedding
- select dart “144“
- execute the “MoveVertex” rule
- select the whole vertex that moved using the correct dart and orbit

select the “48” dart and navigate to the “12” dart (you can select it to see where it is) by using the “Move” function along the correct path of α0, α1 and α2 links (click on the button containing the link you wish to travel under the Move label in the right panel)
close the viewer because in the next lesson you will be running it as a java project

What have you learned?

What is the RGB value of the color embedding of dart “6” of the IcositeHexagon?
Which orbit corresponds to an edge?
Does every orbit correspond to a topological cell?
What is the advantage of embedding the color to a volume face and not a full face?

Lesson 3