Lesson 1: Discover topological structures of Jerboa

Pages

To complete this tutorial you will need to understand how geometric objects are represented and how topological structures work because it is the central notion to using Jerboa to build a geometric modeler. In this lesson you will be using and completing a 3-dimensionnal example modeler made with Jerboa.

For the first two lessons you will use a runnable .Jar file of a modeler developed in Jerboa which you can download here, later on you will install Jerboa so as to modify this modeler.

You may have to set the rights to the jar file (with a « chmod 755 » in the terminal if you are using linux).

Download the Jar

UNDERSTANDING THE TOPOLOGICAL STRUCTURE OF AN OBJECT

The operations which are specific to this lesson can be found in the Lesson1 folder.

execute the « Practice.jar » file
you should see the modeler open
select and apply the “a_TwoCubes” builder to create a simple object (see Screen 1.1) and click on the « Center scene » button

On the left side is a list of operations which you can double click to apply.

The central part of the screen is dedicated to the 3-dimensionnal representation of objects and scenes. You can use the right click to move the point of view and the scroll wheel to zoom in and out.

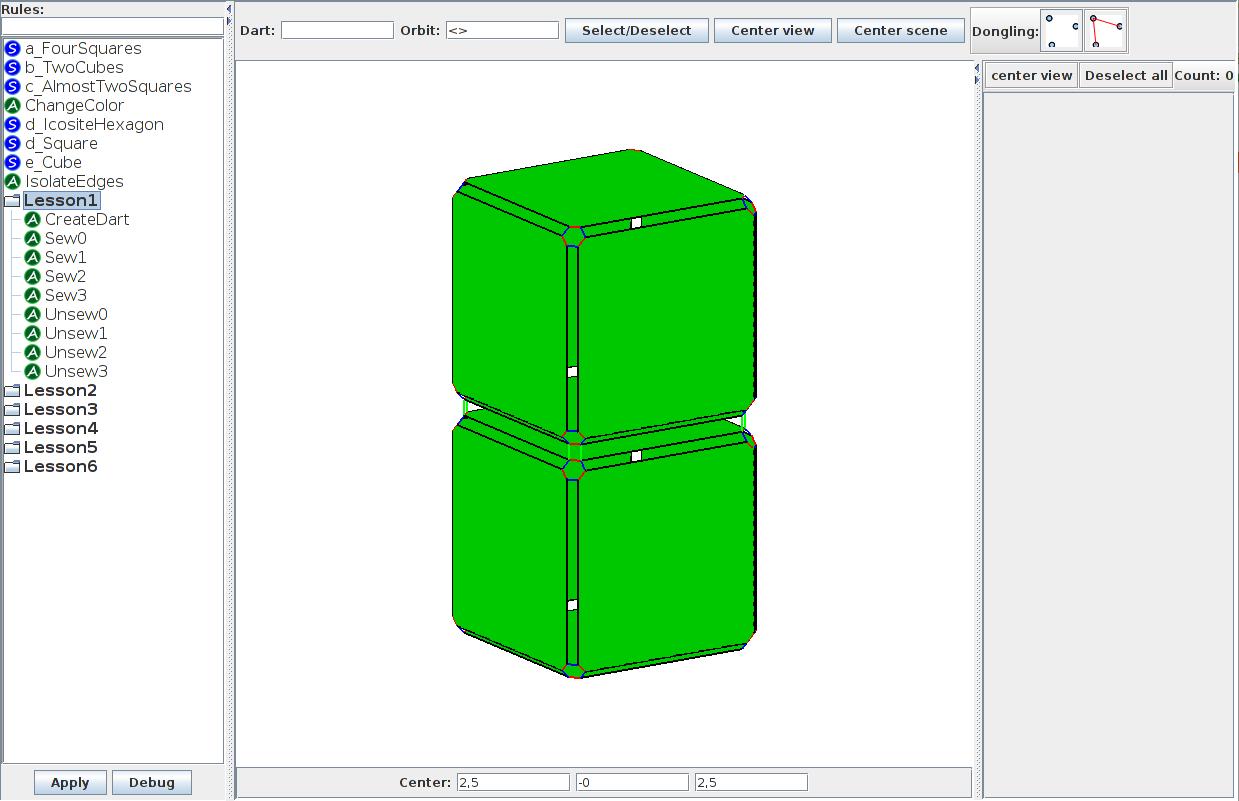
Sorry, you'll have to use your imagination ! — Screen 1.1 : Two Cubes

switch between the exploded (see Screen 1.2) and geometrical (see Screen 1.3) views of the object in the view menu and move around the object to observe the differences between the two views

Notice that the exploded view shows 12 nodes in each corner where the two cubes meet as opposed to the single vertex in the geometrical view.

This is because the topological structure of the object is a graph made up of “darts” (which are the aforementioned nodes of the graph) and different colored “links” (black, red, blue etc – which are arcs of the graph) which represent the different connections between the darts. This graph is called a generalized map (or G-map).

Just above the center you will find the “dart selection tool” which enables you to select any existing dart with its identifying number. You can also select one or more darts using the mouse click but for accuracy reasons, whenever you need to select a particular dart, you will be prompted to do so using this tool. Note that you may have to deselect previously selected darts using the « Deselect all » button on the right of the screen.

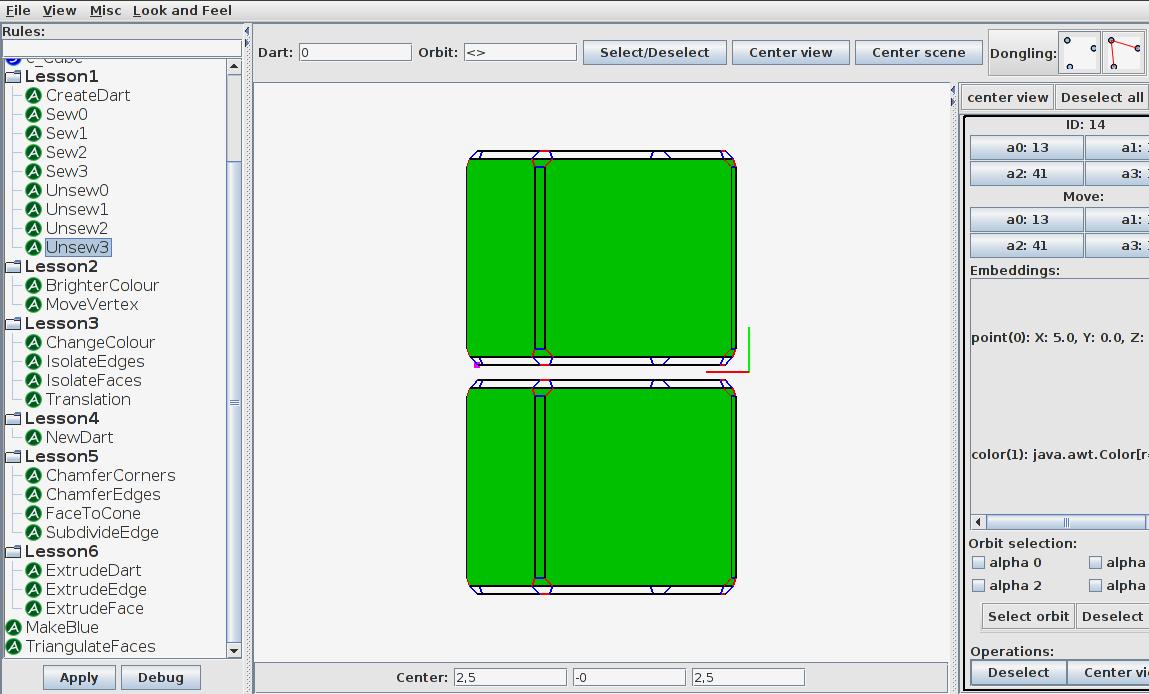
type 14 into the « Dart: » text field and click on « Select/Deselect »
find the selected dart

You will notice that the window to the right of the screen now shows information about the selected dart.

At the top of this window you will find the ID number of the dart and the ID of each neighboring dart along each link (see Screen 1.4).

You can navigate from one dart to the next along a chosen link by clicking on the appropriate link under the « Move » label.

Don’t worry about the rest of the window, we’ll get back to that later.

The two cubes are linked together with links of the 3rd dimension (here called 3-links). You can observe that dart 6 (which is part of the other cube) is adjacent to dart 14 along the 3-link.

Deselect dart 14 and select dart 44 (there is a « Deselect all » button to the right which is very useful)

You will notice that dart 44 is adjacent to itself along the 3-link, this is because there is no dart connected to it with this specific link so the link becomes a « loop ».

Each dart in this 3-dimensionnal modeler has one of each link named from 0 to 3. Each one of these links represents a connection for each topological dimension and is named with the dimension preceded by « alpha », « α » or « a ». On the border of an object the links are represented as loops.

Deselect dart 44

DECONSTRUCTING AN OBJECT

breach the alpha3 links between the two cubes
- use the dart selection tool to select dart “0” which is a dart on the face of a cube which is connected to the face of the other cube
- execute the “Unsew3” rule, you should see the two cubes separated (see Screen 1.5)

breach the alpha2 links to separate a face from one of the cubes
- deselect any selected darts
- use the dart selection tool to select dart “21” which is a dart on one of the faces
- execute the “Unsew2” rule, you should see the face separated from the cube
breach the alpha1 links to separate an edge from the face
- deselect any selected darts
- use the dart selection tool to select dart “22”
- execute the “Unsew1” rule, you should see the edge separated from the face
breach the alpha0 link between the two darts of the separated edge
- leave dart “22” selected
- execute the “Unsew0” rule, you should see the two darts of the edge separated

Notice that the darts, being displayed as infinitely small, are now invisible, you can select them with the dart selection tool to see them highlighted in pink. If you go to « view » and select « show dot » you will be able to see every dart even if it is not connected to anything.

BUILDING AN OBJECT

delete the previous models by going to file, new
build the “b_AlmostTwoCubes” (see Screen 1.6)

connect the lone face to the rest of the cube
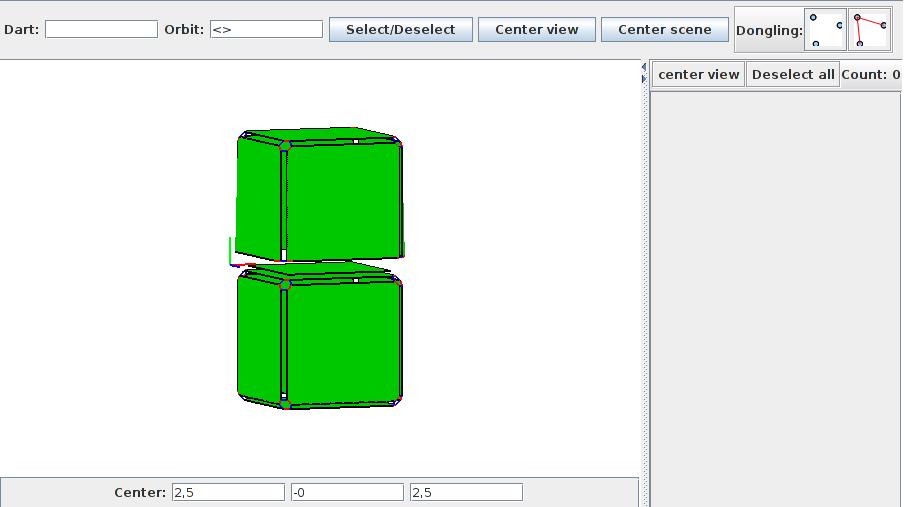
- use the dart selection tool to select darts “11” and “26”
- execute the “Sew2” rule
- repeat with darts « 12 » and « 31 », « 14 » and « 41 », « 9 » and « 51 » remembering to deselect previously selected darts

connect the two cubes with 3-links
- select darts “0” and “8”
- execute the “Sew3” rule, you should have two connected cubes

TOPOLOGICAL CONSTRAINTS

There are three topological constraints which must be respected by a graph to be a G-map:

1- The graph is non-oriented which means that the links don’t have a direction.

2- Each dart has exactly n+1 links, one of each dimension from 0 to the topological dimension n (in our 3D modeler the dimensions of the links go from 0 to 3).

3- For each instance of i and j, where 0<=i<=i+2<=j<=n (n being the dimension of the graph), each dart must have an « i-j-i-j » cycle of links, which means that successively navigating along the links of dimensions i, j, i and j will lead back to the initial dart (even if some links are loops).

Three link cycles must exist for each node on a 3-dimensional graph. These cycles are 0202, 0303 and 1313.

Two faces which are connected by a common corner are thus impossible to represent with a G-map and cannot be built with Jerboa.

select any dart on an object and make sure it has four different links (a0, a1, a2 and a3)
move along the same link twice and make sure you get back to the original dart
navigate along the four links of a cycle and make sure you get back to the original dart

What have you learned?

Does a graph represent the geometric shape of an object?
How many darts are needed to create a square?
Which color is the link for the 2nd topological dimension ?

Lesson 2