Joptopt is a project aiming to study the evolution of volumes under constraints, using generalized maps as a data structure for algorithms. The goal is to exploit the natural relation-based structure of g-maps to facilitate the creation, access, storing and modification of local information in the mesh.
For now, the work made consists in an implementation of the fast marching algorithm (About the fast marching algorithm) over 3D and 2D orthogonal grids and over triangular non obtuse meshes.
Fast Marching Method
Basically, the fast marching method simulates the propagation of a wave on a manifold. It estimate on each point of the manifold the arrival time of the wave by approximating a solution of the following Eikonal equation :
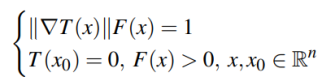
with « T » the arrival time function, « F » a given speed function, « x » a point in the domain, « x0 » a source point of the propagation.
One useful illustration of the fast marching is the example of a forest fire. The fire can have one or multiple sources. The fire spreads at different speed according to the nature of the land. The fire can not spread on an already consumed land, it goes towards new land to burn.
When the fast marching is applied on a mesh, each vertex can be in one of the three following states according to its position relatively to the front propagation :
- FROZEN : equivalent to land already burnt. The front has already passed on this vertex, an arrival time has been estimated and doesn’t change anymore.
- NARROWBAND : equivalent to the current burning land. The front is currently over this vertex. An estimation of the front arrival time has computed but can still change.
- FAR : equivalent to the land not burnt yet. The front hasn’t reached the vertex, its arrival time is equal to « infinite » and will be computed when the front will get closer.
In a synthetic way, the algorithm follows these steps :At the beginning, all the vertices, have an arrival time equal to « infinite » and are in the state « FAR ».
The source of the propagation are chosen, their arrival time is changed to be « 0 », their state is now « FROZEN ». Then the neighbours of the « FROZEN » points are put in the state « NARROWBAND ». While there is vertices in the state « NARROWBAND » we put into the state « FROZEN » the vertex in the « NARROWBAND » with the smallest arrival time value and the arrival time of its neighbours is re-estimated and put into the state « NARROWBAND » (if it’s not already).
Readers interested in the mathematical background of this algorithm should refer to James Sethian and al. works on this topic.
Results
This algorithm is implemented for 2D and 3D orthogonal grids as well as for non obtuse triangular meshes. To do so, the algorithm has been translated into Jerboa’s rules and embeddings. Here are some illustrations of results obtained in Jerboa with the instructions needed to run it in your environnement.

On this figure, the fast marching has been applied with one source located on the flame hold by the statue. The color gradient represent the arrival time value from red (minimum arrival time) to purple (maximal arrival time).
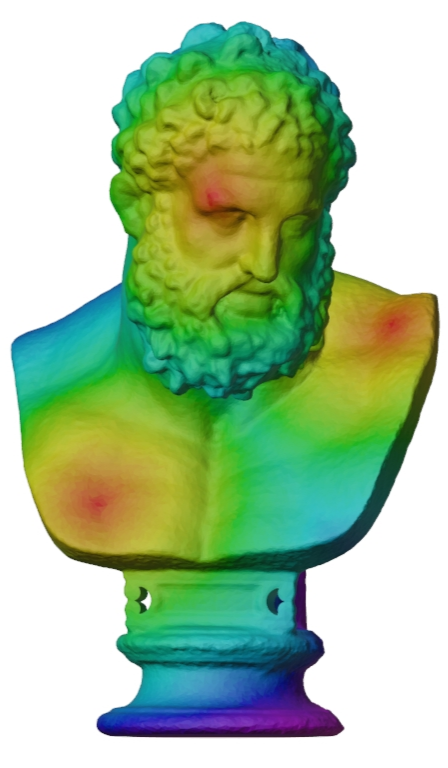


On these figures, the fast marching has been applied with 3 sources for the propagation (« redish » zones). Then the isochrones are shown for different specific times to highlight the topological changes (merges) of the front.
Binary and documentation
This implementation can be found in the following runnable jerboa_fast_marching.jar file. A markdown documentation about the implementation is also available.
In order to run it, it needs a jdk11. For example, I used GraalVM-22.1.0 (https://github.com/graalvm/graalvm-ce-builds/releases). Then run the .jar file with the command java -jar jerboa_fast_marching.jar.
Then, Jerboa visualisez should open, follow the steps in the following video to load a mesh and apply fast marching on it.